Middle Squares

At the theater some years ago, a preview played for Oppenheimer. I’d not heard of the movie before, and nothing about the popular culture suggested to me that a movie like that could be a success. By the end of the preview and for the rest of the feature film (which I’ve forgotten), I wondered whether Oppenhheimer: The Movie would be a trustworthy teller of the real story.

To brush up on the history, I read these two books:

• American Prometheus, a biography of Oppenheimer (I was unaware this book was the movie’s inspiration and motivation)
• The Man from the Future, a biography of John von Neumann, a man whose name appears unusually often alongside phrases like “father of modern computers” and “smartest person ever”. As a student of programming, I’d learned a little about his contributions to computation, and had some passing awareness that he was involved in the Manhattan Project.

This post isn’t about Oppenheimer the man, or even the movie. It’s about an interesting curiosity of the history of random number generators that I learned while reading the Jon von Neumann biography. The biography was worthy of a read despite my expectation of his movie appearance going unfulfilled.

# History

Chapter 5 of The Man from the Future describes his invention of an algorithm for pseudo-random number generation. The story goes something like this.

The Manhattan Project needed to simulate the inside of an atomic weapon. The simulation, using the Monte Carlo method, required more randomly-generated numbers than could ever be fed in on punch cards, as was standard practice at the time. John came up with “middle squares”, a technique for pseudo-random number generation.

Enter Klári von Neumann. She was a mathematician who had met John in Budapest. They married, and ten years later, she joined John in contributing to the Manhattan Project.

Klári tackled the challenge of programming a Monte Carlo simulation of neutron fission to determine the probability spread of quantum events as neutrons traveled inside a nuclear weapon. As far as I know, this was the first PRNG, and Klári wrote the code to implement the algorithm. Klári traveled to Aberdeen to run her program on the ENIAC, but it wasn’t ready for her. It was in the process of being reworked into a stored program computer; if not the first one ever, then certainly the first of such significance.

Looking back, it’s astonishing to reflect on Klári von Neumann becoming a computer programmer seventy-five years, a lifetime, ago. That was twenty years before C, forty years before Java, sixty years before Go, Nodejs, and Rust. In an era where we would consider someone who began programming in the 70s as “extremely early”, writing computer code twenty-three years before that makes her a first member of the first era of the field.

# Method

Klári’s story is worth reading much more about, and is probably more interesting than what this post is supposed to be about: middle-squares.

The method is fairly simple.

1. Start with a seed number
2. Square it
3. Take the middle half of digits as your new random number
4. Use the new number for your purposes, and as the next seed

Something like this.

Where x0 is the initial seed and n is the number of digits.

# Application

Generating numbers randomly has come a long way since 1947, and I’ve no real need, myself, for vast quantities of random numbers. I just don’t work on that kind of program, usually. But I do have this implementation of Ray Tracing in One Weekend I completed while endeavoring to learn Rust. It uses a lot of random numbers, billions and billions. For performance, I implemented here a version of lehmer64. I thought it would be fun to try out middle-squares and see if there were any noticable differences in the rendered image.

Here’s a Rust implementation of middle-squares for u32.

fn middle_squares(seed: u32) -> u32 {
  // square the seed, but first double the
  // width in order to avoid overflow
  let square = (seed as u64).pow(2);
  // cut off 16 bits from the left and right
  let mid = (square >> 16) as u32;
}

It’s simplified in some important ways.

1. This is operating on binary digits, not decimal.
2. It doesn’t consider the number of digits; instead it assumes 64 digits (bits) after squaring. This certainly reduces the longevity of the middle-squares, which is already known to crash to zero after sufficient iterations. This implementation could be improved by using u64::leading_zeroes to help count digits.

Still, it worked!

# Results

Here are some renderings of Ray Tracing in One Weekend, comparing lehmer64 and middle-squares for PRNG.

Original image, using lehmer64.

Middle-squares with a large prime number seed:

Middle-squares looks to perform very well at first glance! Looking closer does reveal some interesting wave patterns. Computer: ENHANCE!

Original (lehmer64):

Middle-squares with wave patterns:

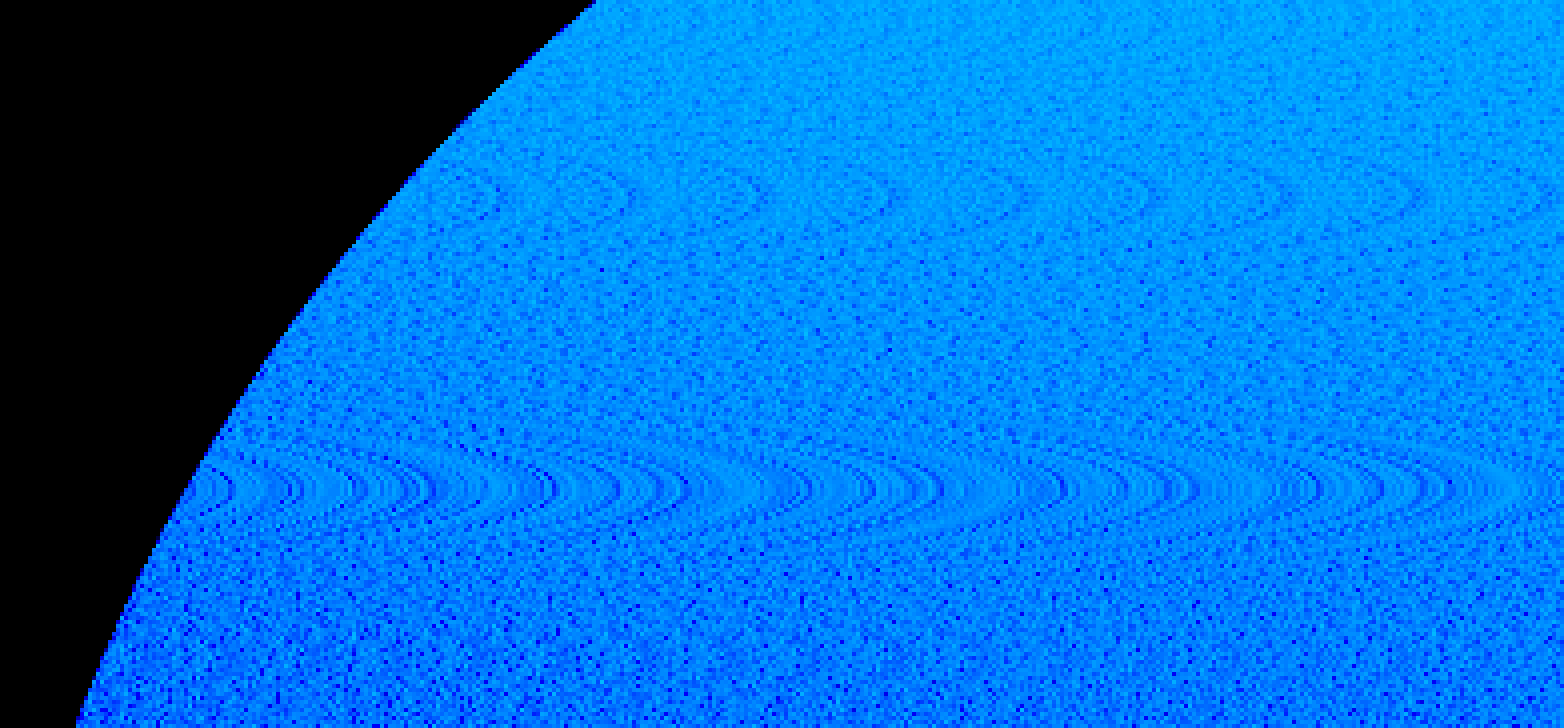
It’s likely that these waves originate are characteristic of my simplified (non-digit-counting) implementation. Or perhaps more likely, my approach of resetting the seed when middle-squares cratered to zero. I didn’t look into it any further, since this was just a fun exercise.

As a last rendering, for fun, here’s middle-squares with a small composite number seed:

Until next time, remember John von Neumann’s reproof:

“Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin.”

# Sources

• For a deep investigation of the Monte Carlo programs created for the Manhattan Project, see Los Alamos Bets on ENIAC: Nuclear Monte Carlo Simulations by Thomas Haigh, Mark Priestley, and Crispin Rope.
• For more on Middle-Squares, see Middle-square method on Wikipedia.
• For John von Neumann’s original paper on Middle-Squares, see Various Techniques Used in Connection With Random Digits, included here for convenience:
  
  
  Browse John von Neumann's paper on Middle Squares